Digital weighing scales: Difference between revisions
| Line 9: | Line 9: | ||
Domestic weighing scales use strain gauges to measure the tiny deformations of a piece of metal under load. | Domestic weighing scales use strain gauges to measure the tiny deformations of a piece of metal under load. | ||
A strain gauge is extremely simple. A zigzag resistive track on a foil backing is elongated and becomes thinner as it is stretched (within its elastic limit), | A strain gauge is extremely simple. A zigzag resistive track on a foil backing is elongated and becomes thinner as it is stretched (within its elastic limit), increasing its resistance. Conversely, if it is compressed (so long as it doesn't buckle), its resistance is reduced. | ||
Foil strain gauges like the one shown are normally very securely glued to a piece of aluminium or steel and covered by a protective layer. This causes them to stretch or be compressed with the metal they are mounted on, however, the change in length is only a fraction of a percent at full load. This translates into a change in resistance typically of | Foil strain gauges like the one shown are normally very securely glued to a piece of aluminium or steel and covered by a protective layer. This causes them to stretch or be compressed with the metal they are mounted on, however, the change in length is only a fraction of a percent at full load. This translates into a percentage change in resistance typically of twice as much since the resistive track is both elongated and thinned as it is stretched. | ||
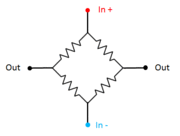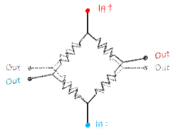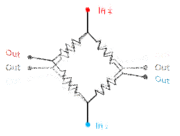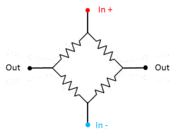
[[File:StrainGaugeAnim.gif|180px|thumb|right|A Wheatstone bridge consisting of 4 strain gauges produces an output when two of them are stretched and the other two compressed.]] | [[File:StrainGaugeAnim.gif|180px|thumb|right|A Wheatstone bridge consisting of 4 strain gauges produces an output when two of them are stretched and the other two compressed.]] | ||
A strain gauge will also change its resistance with temperature, and induced currents from nearby mains electric devices may completely swamp the tiny change in resistance. For these reasons, strain gauges in weighing scales are always used in pairs on opposite sides of a piece of metal, causing one to be stretched while the other is compressed. The difference between their resistances is then measured rather than an absolute resistance, allowing other effects to be cancelled out. | A strain gauge will also change its resistance with temperature, and induced currents from nearby mains electric devices may completely swamp the tiny change in resistance. For these reasons, strain gauges in weighing scales are always used in pairs on opposite sides of a piece of metal, causing one to be stretched while the other is compressed. The difference between their resistances is then measured rather than an absolute resistance, allowing other effects to be cancelled out. | ||
The strain gauges are arranged in a Wheatstone bridge circuit as shown in the animation. A voltage | The strain gauges are normally arranged in a Wheatstone bridge circuit as shown in the animation. A voltage is applied to the top and bottom. Because of the symmetry of the circuit, in the rest position the two output terminals will be at exactly the same voltage, and a voltmeter connected between them would register nothing. But when it is stressed, stretching two opposite strain gauges and compressing the other two, it's put out of balance and a voltage appears between the output terminals. | ||
A bar-type load cell is shown in the photo on the right. This has 2 strain gauges on the top and two on the bottom. | A bar-type load cell is shown in the photo on the right. This has 2 strain gauges on the top and two on the bottom. | ||
At first sight, applying a load to it (the green arrow) would cause the top two strain gauges to be stretched and the lower two to be compressed | At first sight, applying a load to it (the green arrow) would cause the bar to be bent into an arc, causing the top two strain gauges to be stretched and the lower two to be compressed. Furthermore, the lever effect would mean that the amount of stretch or compression would depend on how far from the end of the bar the load was applied. | ||
However, the shaped hole in the middle has two functions: firstly to concentrate the strain into two relatively thin pieces of metal, and secondly to encourage it to bend into an S-shape rather than as arc. As shown by the arrows, S-shape bending will cause two diagonally opposite strain gauges to be stretched and the other two compressed, whereas any tendency to bend into an arc stretches both strain gauges on one side of the Wheatstone bridge and compresses the other two, which doesn't unbalance it. | |||
Digital luggage scales use a load cell following the same principles, but with an S-shaped piece of metal instead of a bar. If you think of the S-shape as two U-shapes joined by one leg, the strain gauges are placed on opposite sides of the bottoms of the two U's. | |||
[[File:Img_1727a.jpg|180px|thumb|left|A half-bridge load cell - top.]] | [[File:Img_1727a.jpg|180px|thumb|left|A half-bridge load cell - top.]] | ||
[[File:Img_1728a.jpg|180px|thumb|right|A half-bridge load cell - bottom.]] | [[File:Img_1728a.jpg|180px|thumb|right|A half-bridge load cell - bottom.]] | ||
The bar-type load cells contain 4 strain gauges in a "full bridge" configuration, but bathroom scales commonly use 4 load cells, each containing just 2 strain gauges on opposite sides of a strip of metal within them. These are known as "half-bridge" load cells and have only 3 wires instead of 4. In this case, the strip is bent into an arc, stretching one strain gauge and compressing the other. They are still wired in a Wheatstone bridge, but each of the 4 arms of the bridge contains 2 strain gauges, one from each of 2 adjacent load cells. The total imbalance of the Wheatstone bridge is then the sum of the imbalances of the 4 load cells, whether or not the load is evenly distributed amongst them. | |||
See [https://learn.sparkfun.com/tutorials/getting-started-with-load-cells Getting Stated with Load Cells]. | See [https://learn.sparkfun.com/tutorials/getting-started-with-load-cells Getting Stated with Load Cells]. | ||
[[Category:Fixing]] | [[Category:Fixing]] | ||
Revision as of 10:03, 26 August 2017
This page covers digital kitchen and bathroom scales. Digital luggage scales follow the same principles of operation.
Summary
There isn't much to go wrong inside digital weighing scales apart from physical problems which should be visible on close inspection. Nevertheless, their principles of operation is interesting, and an understanding will help diagnose any faults which aren't visually obvious.
Principles of operation
Domestic weighing scales use strain gauges to measure the tiny deformations of a piece of metal under load.
A strain gauge is extremely simple. A zigzag resistive track on a foil backing is elongated and becomes thinner as it is stretched (within its elastic limit), increasing its resistance. Conversely, if it is compressed (so long as it doesn't buckle), its resistance is reduced.
Foil strain gauges like the one shown are normally very securely glued to a piece of aluminium or steel and covered by a protective layer. This causes them to stretch or be compressed with the metal they are mounted on, however, the change in length is only a fraction of a percent at full load. This translates into a percentage change in resistance typically of twice as much since the resistive track is both elongated and thinned as it is stretched.
A strain gauge will also change its resistance with temperature, and induced currents from nearby mains electric devices may completely swamp the tiny change in resistance. For these reasons, strain gauges in weighing scales are always used in pairs on opposite sides of a piece of metal, causing one to be stretched while the other is compressed. The difference between their resistances is then measured rather than an absolute resistance, allowing other effects to be cancelled out.
The strain gauges are normally arranged in a Wheatstone bridge circuit as shown in the animation. A voltage is applied to the top and bottom. Because of the symmetry of the circuit, in the rest position the two output terminals will be at exactly the same voltage, and a voltmeter connected between them would register nothing. But when it is stressed, stretching two opposite strain gauges and compressing the other two, it's put out of balance and a voltage appears between the output terminals.
A bar-type load cell is shown in the photo on the right. This has 2 strain gauges on the top and two on the bottom.
At first sight, applying a load to it (the green arrow) would cause the bar to be bent into an arc, causing the top two strain gauges to be stretched and the lower two to be compressed. Furthermore, the lever effect would mean that the amount of stretch or compression would depend on how far from the end of the bar the load was applied.
However, the shaped hole in the middle has two functions: firstly to concentrate the strain into two relatively thin pieces of metal, and secondly to encourage it to bend into an S-shape rather than as arc. As shown by the arrows, S-shape bending will cause two diagonally opposite strain gauges to be stretched and the other two compressed, whereas any tendency to bend into an arc stretches both strain gauges on one side of the Wheatstone bridge and compresses the other two, which doesn't unbalance it.
Digital luggage scales use a load cell following the same principles, but with an S-shaped piece of metal instead of a bar. If you think of the S-shape as two U-shapes joined by one leg, the strain gauges are placed on opposite sides of the bottoms of the two U's.
The bar-type load cells contain 4 strain gauges in a "full bridge" configuration, but bathroom scales commonly use 4 load cells, each containing just 2 strain gauges on opposite sides of a strip of metal within them. These are known as "half-bridge" load cells and have only 3 wires instead of 4. In this case, the strip is bent into an arc, stretching one strain gauge and compressing the other. They are still wired in a Wheatstone bridge, but each of the 4 arms of the bridge contains 2 strain gauges, one from each of 2 adjacent load cells. The total imbalance of the Wheatstone bridge is then the sum of the imbalances of the 4 load cells, whether or not the load is evenly distributed amongst them.